
1%とは何を指すものでしょうか。Wikipediaによると、
偶然性を持つある現象について、その現象が起こることが期待される度合い、あるいは現れることが期待される割合のことをいう。
とのこと。1%とはつまり、100分の1を指すものであり、100ある内の1つ、という意味です。
しかし人というのは自分に都合の良い解釈をするものですね。1%と聞いたら「100回実行したら必ず1回は当たる」と勝手に思い込んでしまうのですから。
こんな言い方をしているのですから、結論はもちろんNO。つまり1%の確率だとしても、100回すべて外れる場合は存在するのです。しかもそれは、意外と高い確率で。
「すっぱいガム」と「コイントス」の違い
駄菓子の「すっぱいガム」を覚えていますでしょうか。3つのガムが入っていて、その内のひとつがとてもすっぱいという、子ども版ロシアンルーレットを楽しめる昔ながらの駄菓子です。
3個のうち1個がすっぱいガム。1つずつ食べていき、3回食べたら必ず当たる。確率は3分の1です。
いっぽうの「コイントス」。コインを投げて表裏の結果を見ます。この場合の表が出る確率は2分の1です。
しかしだからといって「2回実行したら必ず一度は表が出る」というわけではありません。表が出ない場合もありますし、逆に2回とも表である場合もあります。
違いは、引いたものを除外するか否な
この2つの違いはなんでしょうか。確率と同じだけの試行回数が実施しても、当たる場合と、当たらない場合があるのは何故でしょう。
それは「引いたものを除外するか否か」によります。
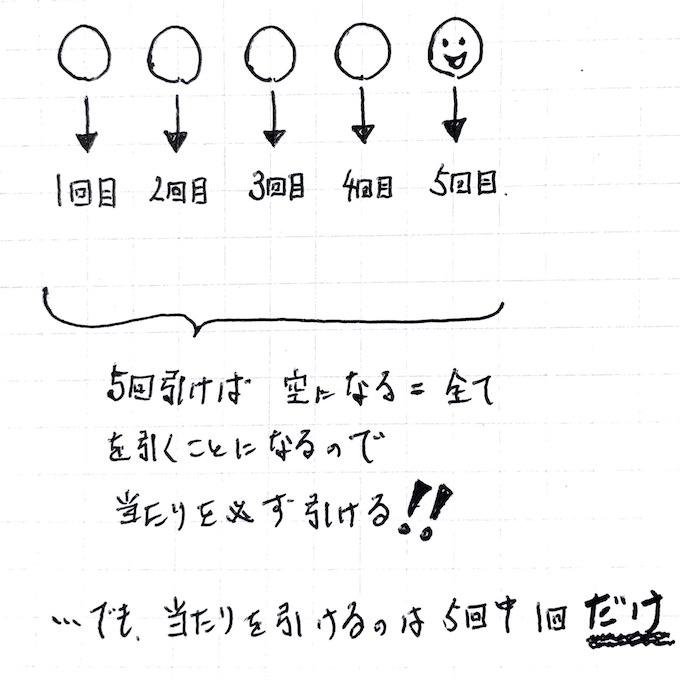
「すっぱいガム」の場合、選択したものを次回の試行時には除外します。
最初の1つを取ったあと、次に取るのは「2つのうちの1つ」。その次に取るのは「最後の1つ」ということになります。
つまり結果はどんどん絞り込まれていき、最後の1つになった時点で確率は100%になるのです。
「コイントス」は違います。
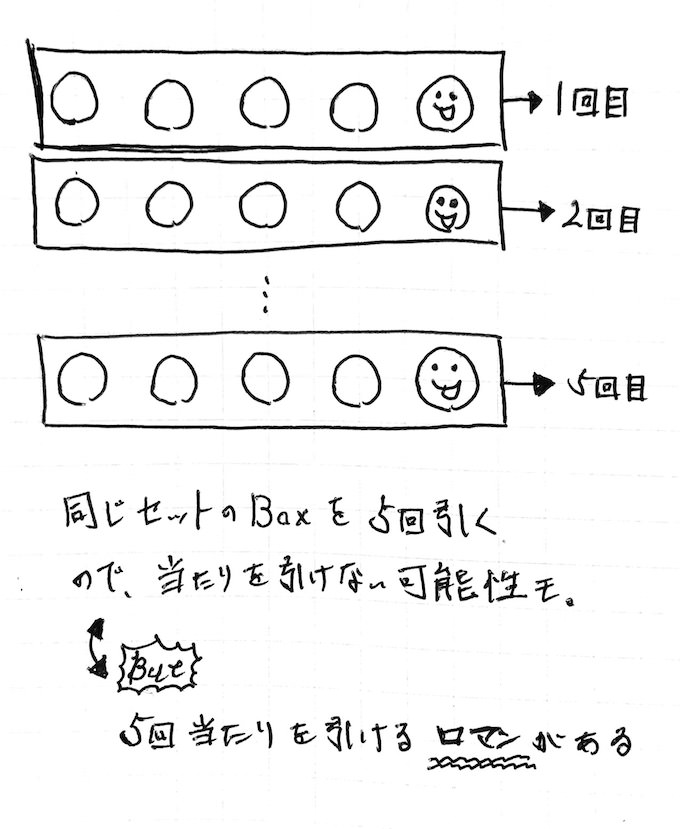
最初の1回を投げる。表が出る。2回目に投げるとき、最初の1回目の結果に関係なく、再度2分の1のコイントスを強要されます。
1回目の結果は、2回目以降に引き継がれず、そのつど条件がリセットされて再度試行が開始されるのです。
これが両社の違い。では電子データである「ガチャ」についてはどうでしょうか。それはもちろん、後者です。
確率 1/3 の当たりクジを 3回引いて、外れる確率は?
例えば確率1/3のガチャがあるとします。
これを3回試行して、目的である「A」を晴れて引ける確率はいくつでしょうか。逆に当たりが引けない確率はいくつでしょうか。
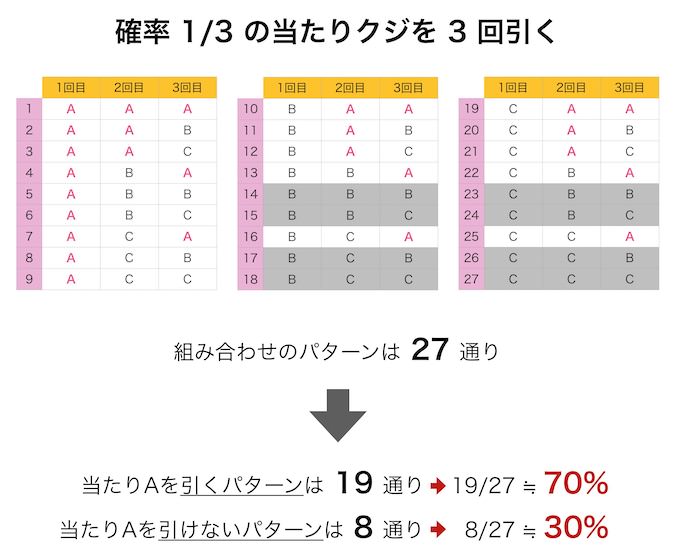
このとき考えるべきは「組み合わせ」。3回の試行で得られる結果のパターンを並べ、その中で当たりの「A」が含まれているケースを計算します。
すると「少なくとも1回は当たりAを引く確率」は、だいたい70%程度だとわかります。
しかし逆に「一度も当たりAを引けない確率」が30%もあることに注目すべきです。
1/n を n回試行すると当たらない確率がどんどん上がる
1/n を n回試行する場合の確率を計算してみると、nの数が大きくなればなるほど、当たりを引けない確率はどんどん上がります。
以下の表は「当たる確率」を計算したもの。試行回数を重ねた分だけ、当たりを引く確率が下がっているのがわかります。
| 1/2 を2回 | 75.00% |
| 1/5 を5回 | 67.23% |
| 1/10 を10回 | 65.13% |
| 1/20 を20回 | 64.15% |
| 1/50 を50回 | 63.58% |
| 1/100 を100回 | 63.40% |
| 1/256 を256回 | 63.28% |
| 1/512 を512回 | 63.25% |
| 1/1024 を1024回 | 63.23% |
現実は甘くない。しかしそこにはロマンがある
数字というのは恐ろしい。一見同じように見えても、結果は全く違うものである。そんな場合があります。
しかし「すっぱいガム」と「コイントス」の決定的で大きな違いがもうひとつあります。
それは「コイントスには、すべて当たりを引けるロマンがある」という点。
試行するたびに条件がリセットされますので、連続で当たりを引ける可能性があります。すべての試行が当たることだってあり得ます。
そういうロマンを追い求めてみるのも、また一興といったところでしょうか。
くれぐれもガチャの課金のしすぎにはご注意くださいね。


